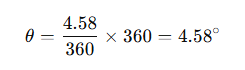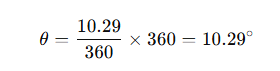No space agencies. No photos from orbit. Just you, the Sun, and a couple of friends.
There’s been a rise in people claiming the Earth is flat, that it’s all a lie, and that organisations like NASA are part of a global conspiracy. Some of these people are trolls chasing clicks, Others may simply have been failed by education. This guide isn’t for the trolls, it’s for those genuinely searching for truth and have lost faith in government institutions and the education system.
If you’re someone who believes the Earth might be flat — or you know someone who does — this experiment is for you. No authorities to trust. No complex equipment. Just some sticks, some friends, the Sun, and your own observations.
Yes, I’m biased — I know the Earth is round. So is the Sun. So is every massive body in the solar system. Gravity makes them that way. But you don’t have to take my word for it. You can test it yourself, there is a simple experiment you and few friends can do by yourself and demonstrate that the Earth is not a flat surface, all you need to two friends – fellow flat Earth believers will do, after all, it’s best to test it together, some equal length poles/sticks and some other equipment – Oh, and a rudimentary understanding of mathematics. So, lets dive in shall we.
This experiment is easy to perform and will give you firsthand evidence that the Earth is round. It relies only on geometry, sunlight, and cooperation between three people. The same method was used by the ancient Greek scientist Eratosthenes over 2,400 years ago.
I do not believe there is any disagreement that a circle can be divided into 360 equal parts, each one a degree, you can do the same on a sphere, where that sphere is a man-made globe or a football (soccer ball to those across the pond). If you know the circumference of that globe, then you can calculate that 1° of the surfaces in any direction will equate to X distance.
Example.
You have a ball/globe that is 360m in circumference (114.57m diameter), you know that you can divide it into 360 equal slices, in either the horizontal or vertical direction from the centre.
360 / 360 = 1m per 1° in either the vertical or the horizontal direction from the centre, there can be no disagreement on this because this is more than 4000-year-old maths.
Now, what you can see if that if you know the distance between two spots on the surface of that sphere, you can do a number of calculations.
- Spot A is at the centre of the globe/sphere and spot B is 4.58m from Spot A, that is horizontally to its right, thus spot A and B are 4.58 ÷ 360 * 360 = 4.580° apart. Calculation of that is simple.
- Spot A is still at the centre of the globe, but spot C is now 10.29m vertically from it, thus it is 10.29÷ 360 * 360 = 10.29° apart. As above, the calculation is simple.
The calculation is always Degrees = (Distance / Circumference) × 360
So, example done with, lets get on with it.
What You’ll Need
- Two friends who live a known distance away, one due south, one due west of you.
- Three vertical poles or sticks of equal height (e.g., broom handles). The ideal is to plant these in the ground and ensure that each has a height of 1m above the ground. They must be of equal height above the ground, or your maths will be inaccurate.
- A sunny day, ideally near the equinox, when the Sun is directly overhead somewhere on the equator, this usually occurs around 20 March and 23rd September each year.
- A GPS app or mapping tool to measure distances. If you have a smart phone, then you can use the GPS data on this or a compass tool.
- A spirit level and plumb line (or level app) to ensure your stick is vertical. The stick/pole must be perfectly vertical
- A protractor or angle finder app to measure shadow angles.
- A watch or solar noon calculator (websites or apps available online).
The Setup
- You are at Point A, the central reference location.
- Ask one friend to position themselves 805 km (500 miles) due south of you (Point B).
- Ask another to position themselves 805 km (500 miles) due west of you (Point C).
Tip: Google Maps or any GPS tool can help you find precise positions.
The Observation
At local solar noon (when the Sun is at its highest point in the sky for each location):
- All three of you place your vertical stick upright on flat ground. It is best to do this about an hour before local Noon and where there are no obvious obstructions to line of site – in the middle of a field is a good place.
- Ensure the pole/stick is level, ensure the top of the stick is 100cm (39 3/8”) from the ground to provide a consistent shadow.
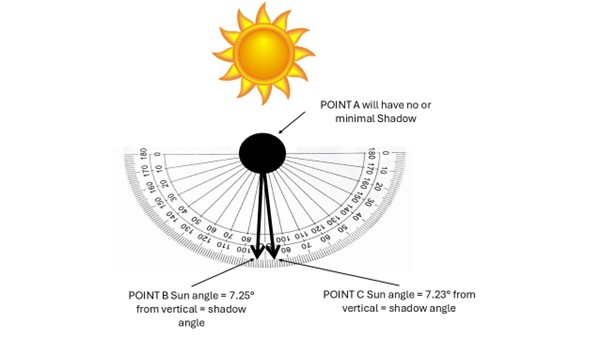
- Measure the angle of the shadow cast by the stick. See the example below.
- At Point A, the Sun should be nearly directly overhead, no shadow (or a very small one).
- At Point B, the shadow will point slightly off north.
- At Point C, the shadow will point east.
Measure the angle between the stick and the Sun at Points B and C using the length of the shadow and basic trigonometry (or an angle app).
The Calculation
You’ll discover:
- At Point B, the Sun is about 7.25° away from vertical.
- At Point C, it’s about 7.23° away.
These angles correspond precisely to the 805 km (500 miles)
Thus, there are
360 / 7.25 = 49.655 * 805 = 39,972.275km (24,383.087 miles)
This is the Polar circumference of the planet, confirming it is a globe.
360 / 7.23 = 49.792 * 805 = 40,082.560km (24,450.361 miles)
This is the Equatorial circumference of the planet, again, confirming it is a globe.
You can doubly confirm your calculations thus.
Your calculated polar diameter of 39,972.275km (24,383.087 miles) means that every degree of the Earth’s surface, when measured from the equator to the poles, is.
39,972.275km (24,383.087 miles) / 360 = 110.534 km (67.42 miles) per 1° of the circle, thus,
805km (500 miles) / 110.534 (67.42 miles) = 7.25°
Equally,
40,082.560km (24,450.361 miles) / 360 = 11.340km (67.917 miles) per 1° of the circle, thus,
805km (500 miles) / 11.340km (67.917 miles) = 7.23°
Try it. You’ll find that it gives you a result of around 40,000 km (24,400 miles), exactly what we’d expect from a globe.
Why This Matters
If Earth were flat:
- All three sticks would cast shadows of the same length and angle, or
- You’d get inconsistent angles that don’t match the distance between locations.
Instead, you’ll get a predictable, consistent curve, which can only happen on a spherical surface.
You Don’t Need to Trust Anyone
This isn’t about believing scientists or governments, it’s about doing an experiment yourself that proves the shape of the Earth using your own tools, your own eyes, and your own brain.
No trickery. No hidden math. No space rockets, you do not even need a computer, the approximate maths can be done on a piece of paper by anyone with basic high school mathematics understanding.
Just sunlight, geometry, and collaboration.
Just to give all a bit of context, as there are many myths that hover around the idea of a flat Earth.
Did Ancient People Really Believe the Earth Was Flat?
Short answer – Mostly no.
The idea that ancient mariners or medieval scholars widely believed the Earth was flat is a modern myth, not a historical reality.
What Did People Actually Believe?
By the time of Eratosthenes (c. 276–194 BCE), the spherical Earth was well understood among educated Greeks. He used shadow lengths in Syene and Alexandria to estimate Earth’s circumference and got surprisingly close to the real value.
But the idea of a round Earth was not exclusive to the ancient Greeks:
- Pythagoras (6th century BCE) is often credited with suggesting Earth was a sphere based on celestial observations.
- Plato and Aristotle supported the spherical Earth model. Aristotle cited lunar eclipses, where Earth’s shadow on the Moon is always round.
- India, texts like the Surya Siddhanta (circa 4th century CE or earlier) describe Earth as a sphere suspended in space.
- Roman and early Islamic scholars also widely accepted a spherical Earth. In fact, many Islamic astronomers refined Eratosthenes’ calculations with several coming within a few 10th of a km of the value used today.
Even in medieval Europe, the idea that people thought Earth was flat is overstated. Most educated individuals, monks, clergy, and scholars knew it was round. But is should be remembered that the educated, during this time, was only a few percent of the total population, which is why many chose to believe the myth.
So Where Did the “Flat Earth” Myth Come From?
The myth gained traction much later:
- 19th century, some writers, especially during debates over science vs. religion, painted the Middle Ages as a time of ignorance, claiming that people believed in a flat Earth. Educated people made claims that history simply does not support, but they were believed sadly.
- One key culprit was Washington Irving, who, in an 1828 fictionalised biography of Columbus, described Spanish clergy arguing that Columbus would sail off the edge. It was a dramatic flourish, not based on reality, n o-one who sailed with Columbus or supported his venture believed in a flat Earth or that they would sail off the edge of the planet.
- Andrew Dickson White and John William Draper, both, well outspoken critics, of organised religion, popularised the idea of a long conflict between science and religion, including the Flat Earth myth as part of their argument. They published books and articles in prestigious publications that supported and repeated the flat Earth myths to support their anti-religious opinions, ironically, ignoring the fact that the Catholic Church, Islam and even the Protestants had never supported the flat Earth Idea.
In short: the flat Earth myth was mostly invented in the 1800s, not believed in the 1400s.
Reality
Ancient mariners didn’t fear falling off the edge of the world, they feared running out of supplies, encountering storms, or sailing into hostile waters that were home to an unknown hostile. The curve of the Earth, visible from the deck of a ship as hulls disappear before masts, was known long before satellites confirmed it, known by the far ancient sailors that have long been lost to history.
The real lesson?
Don’t trust the internet, trust the records, and where you can, do experiments for yourself as detailed above.