Black Holes – The end of Space-Time Jim, but only as we know it!

Black holes are some of the most enigmatic but fascinating objects in the Universe. They appear to be the final chapter in the life of massive stars, packing material in so densely that the gravitational field is so strong that electromagnetic radiation (light to you and me) cannot escape. The point at which this happens is called the Schwarzschild Radius, or commonly referred to as the Event Horizon. The name derives from the German astronomer, Karl Schwarzschild, who calculated this in 1916 as a solution to Einstein’s General Theory of Relativity, published the year before, in which Einstein first predicted the existence of black holes.

The story goes that in December 1967, when these were still theoretical objects, a student reportedly suggested the phrase “black hole” at a lecture by American Astronomer John Wheeler. Wheeler adopted the term for its brevity and it quickly caught on, leading some to credit Wheeler rather than the student. Other terms had been used prior to the 1960’s such as “Dark Star” or “gravitationally collapsed object”, none truly caught on. Black Hole, itself, had been used previously, but it was not widely adopted until after the Wheeler lecture for which he has been credited.

The first Black Hole candidate was not discovered until 1971.

So far, astronomers have identified three types of black holes:

1. Stellar Mass Black Holes: Ranging from 10 to 100 solar masses
2. Intermediate Mass Black Holes: Ranging from 10,000 to 100,000 solar masses
3. Super Massive Black Holes: < 1 million Solar Masses

Lets deal with these very different beasts.

Stellar Mass Black Holes

As we discussed in the article on Supernova, when a star burns through the last of its nuclear fuel it undergoes a core collapse  . For stars from around 8 to 20 times the Sun’s mass they will leave a collapsed core called a neutron star , stars below around 8 solar masses leave a collapsed core called a white dwarf. When stars have a final mass in excess of 25 solar masses it is believed that the final mass of the collapsed core exceeds the Tolman–Oppenheimer–Volkoff  limit of 2.1 Solar Masses, when this happens, as current thinking holds, the core continues to collapse past the Neutron degeneracy point and the end result is a black hole with a mass equivalent to the collapsed core.

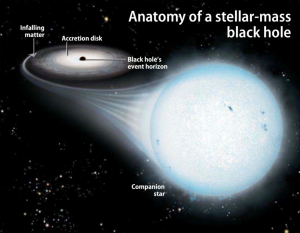
Black holes that formed from the collapse of individual stars are physically very small, astronomically speaking,  but they are incredibly dense. One stellar mass black hole can pack 3 times the mass of the sun into something that is barely larger than a decent mid sized city. The result is a very small, but very intense gravitational field surrounding this object that has an immense pull on anything that comes close enough to be ensnared by it’s gravity.

Any material that strays close enough to the black hole will be captured and pulled into ever tighter orbits, eventually it will be stripped apart, split into individual atoms, heated and inexorably pulled toward the event horizon, from which there is no escape.

As the matter falls toward the event horizon it forms what is called an accretion disk around the equator of the black hole, just as gas and dust form a disk around a star. Once this matter is heated and stripped, it becomes ionised, it glows across the whole electromagnetic spectrum, emitting copious quantities of X-rays and even gamma rays into the surrounding space. As long as there is material falling on the object, it will glow and be detectable, once it has “eaten” all the material in its immediate vicinity, it will go quiet, almost undetectable, until something strays too close and the process starts again, even whole stars can be stripped by these monsters of the dark.

The Harvard-Smithsonian Center for Astrophysics, has stated that in their opinion “the Milky Way contains a few hundred million” stellar mass black holes.

Stellar Mass Black Hole Candidates in the Milky Way

(Links will take readers to Wikipedia pages on the individual object)

Name	BHC mass (Solar Mass)	Companion mass (solar masses )	Orbital Period (days)	Distance from Earth (Light Years)	Location
GRO J0422+32/V518 Per	4 ± 1	1.1	0.21	8500	04:21:43 +32:54:27
GRO J1719-24	≥4.9	~1.6	possibly 0.6	8500	17:19:37 -25:01:03
GX 339-4/V821 Ara	5.8	5–6	1.75	15000	17:02:50 -48:47:23
GRO J1655-40/V1033 Sco	6.3 ± 0.3	2.6–2.8	2.8	5000−11000	16:54:00 -39:50:45
XTE J1118+480/KV UMa	6.8 ± 0.4	6−6.5	0.17	6200	11:18:11 +48:02:13
GRS 1124-683/GU Mus	7.0 ± 0.6		0.43	17000	11:26:27 -68:40:32
XTE J1819-254/V4641 Sgr	7.1 ± 0.3	5–8	2.82	24000 – 40000	18:19:22 -25:24:25
GS 2000+25/QZ Vul	7.5 ± 0.3	4.9–5.1	0.35	8800	20:02:50 +25:14:11
4U 1543-475/IL Lupi	9.4 ± 1.0	0.25	1.1	24000	15:47:09 -47:40:10
XTE J1550-564/V381 Nor	9.6 ± 1.2	6.0–7.5	1.5	17000	15:50:59 -56:28:36
XTE J1650-500	9.7 ± 1.6	.	0.32		16:50:01 -49:57:45
Cyg X-1	11 ± 2	≥18	5.6	6000–8000	19:58:22 +35:12:06
A0620-00/V616 Mon	11 ± 2	2.6–2.8	0.33	3500	06:22:44 -00:20:45
V404 Cyg	12 ± 2	6.0	6.5	7800±460	20:24:04 +33:52:03
GRS 1915+105/V1487 Aql	14 ± 4.0	~1	33.5	40000	19:15:12 +10:56:44
LB-1	68 +11/-13	8	78.9	15000	06:11:49 +22:49:32

Intermediate Mass Black Holes

An intermediate mass black hole (IMBH) is a type with mass in the range 100 to 10,000 solar masses, this is significantly more than stellar mass black holes but dramatically less than the < 1 million solar mass supermassive black holes found in the very heart of large galaxies. A number of IMBH candidate objects have been discovered in our galaxy and other galaxies nearby, this evidence is based on indirect gas cloud velocity and accretion disk spectra observations.

The most compelling evidence for IMBHs comes from a handful of low-luminosity active galactic nuclei. Astronomers believe that because of their observed activity these galaxies contain black holes that are actively accreting material from their surroundings. An example of one such IMBH is a spiral galaxy, NGC 4395, at a distance of about 13 million light years (4 Million parsecs) appears to contain a black hole with mass of about 36,000 solar masses.

Astronomers further believe that some ultra-luminous X ray sources in nearby galaxies are suspected to be intermediate mass black holes, with masses in the range of a 100 to a 1000 solar masses. These intermediate black holes are observed in star-forming regions, such as in the starburst galaxy M82, and are appear associated with young star clusters , also common in these areas of galaxies. The only way to be sure is to undertake a dynamic mass measurement based on the orbit of any binary star orbiting the suspected intermediate mass black hole, and this is far from a simple task, especially given the distances and associated angular separation of these objects.

Astronomers have suggested a handful of  globular clusters may contain intermediate mass black holes, these claims are based on measurements of the velocities of stars near the centre of the globular cluster.  To date, none of these candidates have stood up to further scrutiny and their existence is still unconfirmed. Some of the objects claimed to exist, such as one in the globular cluster M31-G1, (a companion of the galaxy M31) are not required to explain the movement and the velocity of the stars within the cluster.

So where did these Intermediate Mass Black Holes come from, they are too big to be from collapsed stars, and too small to be at the cores of galaxies, so we have a mystery, one yet, we do not know the answer too.

The theories as to their origins can be broken down into three basic premises;

1. They formed at the start of the Universe immediately after the big bang.
2. They formed from the merger of multiple stellar mass black holes and other compact objects (Neutron stars and white dwarves) as well as the accretion of material from supergiant stars.
3. They form from the direct collision of supermassive stars in dense stellar clusters, such as globular clusters and the accretion of material from their surroundings.

Research continues to discover confirmed Intermediate mass black holes, but whilst there are an increasing list of candidates, none have, so far, been confirmed, though many claimed.

Super-Massive Black Hole (SMBH)

So called super-massive black holes (SMBH) is the largest class of black hole, these have a mass ranging from a few 100,000’s to billions of times the mass of our Sun. It is believed these were formed in the very earliest moments of the aftermath of the big bang or shortly after from the collapse and merger of supermassive stars.

Observational evidence indicates that nearly all large galaxies contain a super-massive black hole, located at the galaxy’s centre. In the case of the Milky Way, the supermassive black hole corresponds to the location of Sagittarius A* at the Galactic Core. It is believed that accretion of interstellar gas, from collisions with stars, and possibly other black holes with supermassive black holes is the process responsible for powering quasars and other types of active galactic nuclei.

Super-massive black holes have properties that distinguish them from lower-mass classifications. First, the average density of a SMBH (defined as the mass of the black hole divided by the volume within its Schwarzschild radius) can be less than the density of water. This is because the Schwarzschild radius is directly proportional to its mass, and since the volume of a spherical object is directly proportional to the cube of the radius, the density of a black hole is inversely proportional to the square of the mass, and thus higher mass black holes have lower average density. In addition, the tidal forces in the vicinity of the event horizon are significantly weaker for supermassive black holes. The tidal force on a body at the event horizon is likewise inversely proportional to the square of the mass. A person on the surface of the Earth and one at the event horizon of a 10 million black hole experience about the same tidal force between their head and feet. Unlike with stellar mass black holes, one would not experience significant tidal force until very deep into the black hole.

Some astronomers have begun labelling black holes of at least 10 billion solar masses as ultra-massive black holes. Most of these (such as TON 618) are associated with exceptionally energetic quasars.

What is the Schwartzschild Radius or Event Horizon?

The Schwarzschild radius is a physical parameter that shows up in the Schwarzschild solution to Einstein’s field equations, this corresponds to the radius defining the event horizon, the point at which the escape velocity of the black hole exceeds the speed of light, and thus, not even light can cross,  of a black hole.

The Schwarzschild radius was named after the German astronomer Karl Schwarzschild, who calculated this a solution 1916 in response to the field equations in Einstein’s General Relativity, which had been published the year before.

The Schwarzschild radius is given as

where G is the gravitational constant,

M is the object mass

c is the speed of light in a vacuum. (299,792.458 km/s or 299,792,458 m/s)

The Schwarzschild radius of an object is proportional to the mass. Accordingly, the Sun has a Schwarzschild radius of approximately 3.0 km (1.9 mi), whereas Earth’s is only about 9 mm (0.35 in) and the Moon’s is about 0.1 mm (0.0039 in). The observable universe’s mass has a Schwarzschild radius of approximately 13.7 billion light-years.

If an object has a  radius smaller than its calculated Schwarzschild radius then it is, by definition, a black hole. The surface at the Schwarzschild radius acts as an event horizon in a non-rotating body (a rotating black hole operates slightly differently). Neither light nor particles can pass back through this surface  once they cross within.

Anatomy of a Black Hole.

Singularity

At the centre of a black hole, as described by general relativity, may lie a gravitational singularity, a region where the spacetime curvature becomes infinite. For a non-rotating black hole, this region takes the shape of a single point and for a rotating black hole, it is smeared out to form a ring singularity that lies in the plane of rotation. In both cases, the singular region has zero volume. It can also be shown that the singular region contains all the mass of the black hole solution. The singular region can thus be thought of as having infinite density.

Photon sphere

The photon sphere is a spherical boundary of zero thickness in which photons that move on tangents to that sphere would be trapped in a circular orbit around the black hole.

For non-rotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius. Their orbits would be dynamically unstable, hence any small perturbation, such as a particle of in-falling matter, would cause an instability that would grow over time, either setting the photon on an outward trajectory causing it to escape the black hole, or on an inward spiral where it would eventually cross the event horizon.

Ergosphere

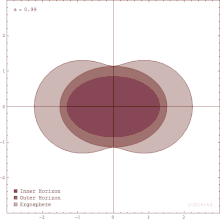
Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere. This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly “drag” along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole, this effect is so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.

The ergosphere of a black hole is a volume whose inner boundary is the black hole’s oblate spheroid event horizon and a pumpkin-shaped outer boundary, which coincides with the event horizon at the poles but noticeably wider around the equator. The outer boundary is sometimes called the ergosurface.

Objects and radiation can escape normally from the ergosphere. Through the Penrose process, named for Roger Penrose who calculated it, objects can emerge from the ergosphere with more energy than they entered. This energy is taken from the rotational energy of the black hole causing the latter to slow.

In the presence of strong magnetic fields, a variation of the Penrose process, the Blandford–Znajek process, is considered the most likely mechanism for the enormous luminosity and relativistic jets of quasars and other active galactic nuclei.

 

The Event Horizon

The defining feature of a black hole is the appearance of an event horizon—a boundary in space-time through which matter and light can pass only inward towards the mass of the black hole. Nothing, not even light, can escape from inside the event horizon. The event horizon is referred to as such because if an event occurs within the boundary, information from that event cannot reach an outside observer, making it impossible to determine whether such an event occurred.

As predicted by general relativity, the presence of a mass deforms space-time in such a way that the paths taken by particles bend towards the mass.At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.

To a distant observer, clocks near a black hole would appear to tick more slowly than those further away from the black hole. Due to this effect, known as gravitational time dilation, an object falling into a black hole appears to slow as it approaches the event horizon, taking an infinite time to reach it.^[ At the same time, all processes on this object slow down, from the view point of a fixed outside observer, causing any light emitted by the object to appear redder and dimmer, an effect known as gravitational red-shift. Eventually, the falling object fades away until it can no longer be seen. Typically this process happens very rapidly with an object disappearing from view within less than a second.

On the other hand, indestructible observers falling into a black hole do not notice any of these effects as they cross the event horizon. According to their own clocks, which appear to them to tick normally, they cross the event horizon after a finite time without noting any singular behaviour; in classical general relativity, it is impossible to determine the location of the event horizon from local observations, due to Einstein’s equivalence principle.

The shape of the event horizon of a black hole is always approximately spherical. For non-rotating (static) black holes the geometry of the event horizon is precisely spherical, while for rotating black holes the event horizon is oblate

Evaporation

In 1974, the late Stephen Hawking mathematically predicted that black holes  emit small amounts of thermal radiation, this has become known as Hawking radiation.

By applying quantum field theory to a static black hole background, he determined that a black hole should emit particles that display a perfect black body spectrum. Since Hawking’s publication, many others have verified the result through various approaches. If Hawking’s theory of black hole radiation is correct, then black holes are expected to shrink and evaporate over time as they lose mass by the emission of photons and other particles.

The Hawking temperature, the point at which the black hole emits radiation, is proportional to the surface gravity of the black hole, which, for a Schwarzschild black hole (none rotating), is inversely proportional to the mass. Hence, large black holes would emit less radiation than small black holes.

A stellar black mass hole of 1 solar mass has a Hawking temperature of ~0.0000000062 kelvins. This is far less than the 2.7 K temperature of the cosmic microwave background radiation. Stellar mass, or larger black holes, receive more mass from the cosmic microwave background than they lose from the emission of Hawking radiation, thus will always grow.

To have a Hawking temperature larger than 2.7 K, and thus be able to evaporate, a black hole would need a mass less than the Moon (7.34767309 × 10²² kilograms), or 1/80th Earth’s mass, however,  a black hole this small would have a Schwarzschild radius of less than a tenth of a millimetre.

If a black hole is very small, the radiation effects are expected to become very strong. A black hole with the mass of a car would have a diameter of about 10⁻²⁴ m and take a nanosecond to evaporate, during which time it would briefly have a luminosity of more than 200 times that of the Sun.

For such a small black hole, quantum gravitation effects are expected to play an important role and could hypothetically make such a small black hole stable, although current research in the impacts of quantum gravity do not indicate this is the case.

The Hawking radiation for an astrophysical black hole is predicted to be very weak and would thus be exceedingly difficult to detect from Earth. A possible exception, however, is the burst of gamma rays emitted in the last stage of the evaporation of primordial black holes. Searches for such flashes have proven unsuccessful.

NASA’s Fermi Gamma-ray Space Telescope, launched in 2008, will continue the search for these flashes. If black holes evaporate via Hawking radiation, a solar mass black hole will evaporate, a process that cannot start until the temperature of the cosmic microwave background drops below that of the black hole, over a period of 10⁶⁴ years, a time span significantly longer than the life of the Universe to date.

A supermassive black hole with a mass of 10¹¹ (100 billion)solar masses  will evaporate in around 2×10¹⁰⁰ years. Some monster black holes in the universe are predicted to continue to grow up to perhaps 10¹⁴ solar masses during the collapse of super clusters of galaxies. Even these would evaporate over a timescale of up to 10¹⁰⁶ years.